Association rule learning
In data mining, association rule learning is a popular and well researched method for discovering interesting relations between variables in large databases. Piatetsky-Shapiro[1] describes analyzing and presenting strong rules discovered in databases using different measures of interestingness. Based on the concept of strong rules, Agrawal et al.[2] introduced association rules for discovering regularities between products in large scale transaction data recorded by point-of-sale (POS) systems in supermarkets. For example, the rule 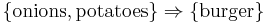 found in the sales data of a supermarket would indicate that if a customer buys onions and potatoes together, he or she is likely to also buy hamburger meat. Such information can be used as the basis for decisions about marketing activities such as, e.g., promotional pricing or product placements. In addition to the above example from market basket analysis association rules are employed today in many application areas including Web usage mining, intrusion detection and bioinformatics.
found in the sales data of a supermarket would indicate that if a customer buys onions and potatoes together, he or she is likely to also buy hamburger meat. Such information can be used as the basis for decisions about marketing activities such as, e.g., promotional pricing or product placements. In addition to the above example from market basket analysis association rules are employed today in many application areas including Web usage mining, intrusion detection and bioinformatics.
Contents |
Definition
| transaction ID | milk | bread | butter | beer |
|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 |
| 4 | 1 | 1 | 1 | 0 |
| 5 | 0 | 1 | 0 | 0 |
Following the original definition by Agrawal et al.[2] the problem of association rule mining is defined as: Let 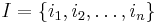 be a set of
be a set of  binary attributes called items. Let
binary attributes called items. Let 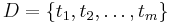 be a set of transactions called the database. Each transaction in
be a set of transactions called the database. Each transaction in  has a unique transaction ID and contains a subset of the items in
has a unique transaction ID and contains a subset of the items in  . A rule is defined as an implication of the form
. A rule is defined as an implication of the form 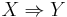 where
where 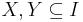 and
and 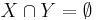 . The sets of items (for short itemsets)
. The sets of items (for short itemsets)  and
and  are called antecedent (left-hand-side or LHS) and consequent (right-hand-side or RHS) of the rule respectively.
are called antecedent (left-hand-side or LHS) and consequent (right-hand-side or RHS) of the rule respectively.
To illustrate the concepts, we use a small example from the supermarket domain. The set of items is 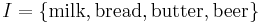 and a small database containing the items (1 codes presence and 0 absence of an item in a transaction) is shown in the table to the right. An example rule for the supermarket could be
and a small database containing the items (1 codes presence and 0 absence of an item in a transaction) is shown in the table to the right. An example rule for the supermarket could be 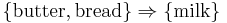 meaning that if butter and bread is bought, customers also buy milk.
meaning that if butter and bread is bought, customers also buy milk.
Note: this example is extremely small. In practical applications, a rule needs a support of several hundred transactions before it can be considered statistically significant, and datasets often contain thousands or millions of transactions.
Useful Concepts
To select interesting rules from the set of all possible rules, constraints on various measures of significance and interest can be used. The best-known constraints are minimum thresholds on support and confidence.
- The support
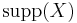 of an itemset
of an itemset  is defined as the proportion of transactions in the data set which contain the itemset. In the example database, the itemset
is defined as the proportion of transactions in the data set which contain the itemset. In the example database, the itemset 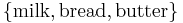 has a support of
has a support of  since it occurs in 20% of all transactions (1 out of 5 transactions).
since it occurs in 20% of all transactions (1 out of 5 transactions).
- The confidence of a rule is defined
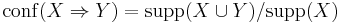 . For example, the rule
. For example, the rule 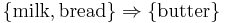 has a confidence of
has a confidence of 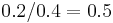 in the database, which means that for 50% of the transactions containing milk and bread the rule is correct.
in the database, which means that for 50% of the transactions containing milk and bread the rule is correct.
- Confidence can be interpreted as an estimate of the probability
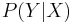 , the probability of finding the RHS of the rule in transactions under the condition that these transactions also contain the LHS.[3]
, the probability of finding the RHS of the rule in transactions under the condition that these transactions also contain the LHS.[3]
- Confidence can be interpreted as an estimate of the probability
- The lift of a rule is defined as
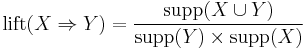 or the ratio of the observed support to that expected if X and Y were independent. The rule
or the ratio of the observed support to that expected if X and Y were independent. The rule 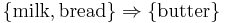 has a lift of
has a lift of 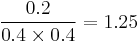 .
.
- The conviction of a rule is defined as
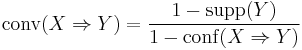 . The rule
. The rule 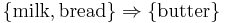 has a conviction of
has a conviction of 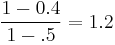 , and can be interpreted as the ratio of the expected frequency that X occurs without Y (that is to say, the frequency that the rule makes an incorrect prediction) if X and Y were independent divided by the observed frequency of incorrect predictions. In this example, the conviction value of 1.2 shows that the rule
, and can be interpreted as the ratio of the expected frequency that X occurs without Y (that is to say, the frequency that the rule makes an incorrect prediction) if X and Y were independent divided by the observed frequency of incorrect predictions. In this example, the conviction value of 1.2 shows that the rule 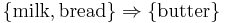 would be incorrect 20% more often (1.2 times as often) if the association between X and Y was purely random chance.
would be incorrect 20% more often (1.2 times as often) if the association between X and Y was purely random chance.
- The property of succinctness(Characterized by clear, precise expression in few words) of a constraint. A constraint is succinct if we are able to explicitly write down all Item-sets,that satisfy the constraint.
Example : Constraint C = S.Type = {NonFood}
Products that would satisfy this constraint are for ex. {Headphones,Shoes,Toilet paper}
Usage Example: Instead of using Apriori algorithm to obtain the Frequent-Item-sets we can instead create all the Item-sets and run support counting only once.
Process
Association rules are usually required to satisfy a user-specified minimum support and a user-specified minimum confidence at the same time. Association rule generation is usually split up into two separate steps:
- First, minimum support is applied to find all frequent itemsets in a database.
- Second, these frequent itemsets and the minimum confidence constraint are used to form rules.
While the second step is straight forward, the first step needs more attention.
Finding all frequent itemsets in a database is difficult since it involves searching all possible itemsets (item combinations). The set of possible itemsets is the power set over  and has size
and has size 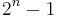 (excluding the empty set which is not a valid itemset). Although the size of the powerset grows exponentially in the number of items
(excluding the empty set which is not a valid itemset). Although the size of the powerset grows exponentially in the number of items  in
in  , efficient search is possible using the downward-closure property of support[2][4] (also called anti-monotonicity[5]) which guarantees that for a frequent itemset, all its subsets are also frequent and thus for an infrequent itemset, all its supersets must also be infrequent. Exploiting this property, efficient algorithms (e.g., Apriori[6] and Eclat[7]) can find all frequent itemsets.
, efficient search is possible using the downward-closure property of support[2][4] (also called anti-monotonicity[5]) which guarantees that for a frequent itemset, all its subsets are also frequent and thus for an infrequent itemset, all its supersets must also be infrequent. Exploiting this property, efficient algorithms (e.g., Apriori[6] and Eclat[7]) can find all frequent itemsets.
History
The concept of association rules was popularised particularly due to the 1993 article of Agrawal,[2] which has acquired more than 6000 citations according to Google Scholar, as of March 2008, and is thus one of the most cited papers in the Data Mining field. However, it is possible that what is now called "association rules" is similar to what appears in the 1966 paper[8] on GUHA, a general data mining method developed by Petr Hájek et al.[9]
Alternative measures of interestingness
Next to confidence also other measures of interestingness for rules were proposed. Some popular measures are:
- All-confidence[10]
- Collective strength[11]
- Conviction[12]
- Leverage[13]
- Lift (originally called interest)[12]
A definition of these measures can be found here. Several more measures are presented and compared by Tan et al.[14] Looking for techniques that can model what the user has known (and using this models as interestingness measures) is currently an active research trend under the name of "Subjective Interestingness"
Statistically sound associations
One limitation of the standard approach to discovering associations is that by searching massive numbers of possible associations to look for collections of items that appear to be associated, there is a large risk of finding many spurious associations. These are collections of items that co-occur with unexpected frequency in the data, but only do so by chance. For example, suppose we are considering a collection of 10,000 items and looking for rules containing two items in the left-hand-side and 1 item in the right-hand-side. There are approximately 1,000,000,000,000 such rules. If we apply a statistical test for independence with a significance level of 0.05 it means there is only a 5% chance of accepting a rule if there is no association. If we assume there are no associations, we should nonetheless expect to find 50,000,000,000 rules. Statistically sound association discovery[15][16] controls this risk, in most cases reducing the risk of finding any spurious associations to a user-specified significance level.
Algorithms
Many algorithms for generating association rules were presented over time.
Some well known algorithms are Apriori, Eclat and FP-Growth, but they only do half the job, since they are algorithms for mining frequent itemsets. Another step needs to be done after to generate rules from frequent itemsets found in a database.
Apriori algorithm
Apriori[6] is the best-known algorithm to mine association rules. It uses a breadth-first search strategy to counting the support of itemsets and uses a candidate generation function which exploits the downward closure property of support.
Eclat algorithm
Eclat[7] is a depth-first search algorithm using set intersection.
FP-growth algorithm
FP-growth (frequent pattern growth)[17] uses an extended prefix-tree (FP-tree) structure to store the database in a compressed form. FP-growth adopts a divide-and-conquer approach to decompose both the mining tasks and the databases. It uses a pattern fragment growth method to avoid the costly process of candidate generation and testing used by Apriori.
GUHA procedure ASSOC
GUHA is a general method for exploratory data analysis that has theoretical foundations in observational calculi.[18] The ASSOC procedure[19] is a GUHA method which mines for generalized association rules using fast bitstrings operations. The association rules mined by this method are more general than those output by apriori, for example "items" can be connected both with conjunction and disjunctions and the relation between antecedent and consequent of the rule is not restricted to setting minimum support and confidence as in apriori: an arbitrary combination of supported interest measures can be used.
OPUS search
OPUS is an efficient algorithm for rule discovery that, in contrast to most alternatives, does not require either monotone or anti-monotone constraints such as minimum support.[20] Initially used to find rules for a fixed consequent[20][21] it has subsequently been extended to find rules with any item as a consequent.[22] OPUS search is the core technology in the popular Magnum Opus association discovery system.
Lore
A famous story about association rule mining is the "beer and diaper" story. A purported survey of behavior of supermarket shoppers discovered that customers (presumably young men) who buy diapers tend also to buy beer. This anecdote became popular as an example of how unexpected association rules might be found from everyday data. There are varying opinions as to how much of the story is true.[23] Daniel Powers says[23]
In 1992, Thomas Blischok, manager of a retail consulting group at Teradata, and his staff prepared an analysis of 1.2 million market baskets from about 25 Osco Drug stores. Database queries were developed to identify affinities. The analysis "did discover that between 5:00 and 7:00 p.m. that consumers bought beer and diapers". Osco managers did NOT exploit the beer and diapers relationship by moving the products closer together on the shelves.
Other types of association mining
Contrast set learning is a form of associative learning. Contrast set learners use rules that differ meaningfully in their distribution across subsets.[24]
Weighted class learning is another form of associative learning in which weight may be assigned to classes to give focus to a particular issue of concern for the consumer of the data mining results.
K-optimal pattern discovery provides an alternative to the standard approach to association rule learning that requires that each pattern appear frequently in the data.
Mining frequent sequences uses support to find sequences in temporal data.[25]
Generalized Association Rules hierarchical taxonomy (concept hierarchy)
Quantitiative Association Rules categorical and quantitative data
Interval Data Association Rules e.g. partition the age into 5-year-increment ranged
Maximal Association Rules
Sequential Association Rules temporal data e.g. first buy computer, then CD Roms, then a webcam.
See also
References
- ^ Piatetsky-Shapiro, G. (1991), Discovery, analysis, and presentation of strong rules, in G. Piatetsky-Shapiro & W. J. Frawley, eds, ‘Knowledge Discovery in Databases’, AAAI/MIT Press, Cambridge, MA.
- ^ a b c d e R. Agrawal; T. Imielinski; A. Swami: Mining Association Rules Between Sets of Items in Large Databases", SIGMOD Conference 1993: 207-216
- ^ Jochen Hipp, Ulrich Güntzer, and Gholamreza Nakhaeizadeh. Algorithms for association rule mining - A general survey and comparison. SIGKDD Explorations, 2(2):1-58, 2000.
- ^ Tan, Pang-Ning; Michael, Steinbach; Kumar, Vipin (2005). "Chapter 6. Association Analysis: Basic Concepts and Algorithms". Introduction to Data Mining. Addison-Wesley. ISBN 0321321367. http://www-users.cs.umn.edu/~kumar/dmbook/ch6.pdf.
- ^ Jian Pei, Jiawei Han, and Laks V.S. Lakshmanan. Mining frequent itemsets with convertible constraints. In Proceedings of the 17th International Conference on Data Engineering, April 2–6, 2001, Heidelberg, Germany, pages 433-442, 2001.
- ^ a b Rakesh Agrawal and Ramakrishnan Srikant. Fast algorithms for mining association rules in large databases. In Jorge B. Bocca, Matthias Jarke, and Carlo Zaniolo, editors, Proceedings of the 20th International Conference on Very Large Data Bases, VLDB, pages 487-499, Santiago, Chile, September 1994.
- ^ a b Mohammed J. Zaki. Scalable algorithms for association mining. IEEE Transactions on Knowledge and Data Engineering, 12(3):372-390, May/June 2000.
- ^ Hajek P., Havel I., Chytil M.: The GUHA method of automatic hypotheses determination, Computing 1(1966) 293-308.
- ^ Petr Hajek, Tomas Feglar, Jan Rauch, David Coufal. The GUHA method, data preprocessing and mining. Database Support for Data Mining Applications, ISBN 978-3-540-22479-2, Springer, 2004
- ^ Edward R. Omiecinski. Alternative interest measures for mining associations in databases. IEEE Transactions on Knowledge and Data Engineering, 15(1):57-69, Jan/Feb 2003.
- ^ C. C. Aggarwal and P. S. Yu. A new framework for itemset generation. In PODS 98, Symposium on Principles of Database Systems, pages 18-24, Seattle, WA, USA, 1998.
- ^ a b Sergey Brin, Rajeev Motwani, Jeffrey D. Ullman, and Shalom Tsur. Dynamic itemset counting and implication rules for market basket data. In SIGMOD 1997, Proceedings ACM SIGMOD International Conference on Management of Data, pages 255-264, Tucson, Arizona, USA, May 1997.
- ^ Piatetsky-Shapiro, G., Discovery, analysis, and presentation of strong rules. Knowledge Discovery in Databases, 1991: p. 229-248.
- ^ Pang-Ning Tan, Vipin Kumar, and Jaideep Srivastava. Selecting the right objective measure for association analysis. Information Systems, 29(4):293-313, 2004.
- ^ Webb, G.I. (2007). Discovering Significant Patterns. Machine Learning 68(1). Netherlands: Springer, pages 1-33. online access
- ^ A. Gionis, H. Mannila, T. Mielikainen, and P. Tsaparas, Assessing Data Mining Results via Swap Randomization, ACM Transactions on Knowledge Discovery from Data (TKDD), Volume 1 , Issue 3 (December 2007) Article No. 14.
- ^ Jiawei Han, Jian Pei, Yiwen Yin, and Runying Mao. Mining frequent patterns without candidate generation. Data Mining and Knowledge Discovery 8:53-87, 2004.
- ^ J. Rauch, Logical calculi for knowledge discovery in databases. Proceedings of the First European Symposium on Principles of Data Mining and Knowledge Discovery, Springer, 1997, pgs. 47-57.
- ^ Hájek, P.; Havránek P (1978). Mechanising Hypothesis Formation – Mathematical Foundations for a General Theory. Springer-Verlag. ISBN 0-7869-1850-8. http://www.cs.cas.cz/hajek/guhabook/.
- ^ a b Webb, G. I. (1995). OPUS: An Efficient Admissible Algorithm For Unordered Search. Journal of Artificial Intelligence Research 3. Menlo Park, CA: AAAI Press, pages 431-465 online access.
- ^ Bayardo, R.J.; Agrawal, R.; Gunopulos, D. (2000). "Constraint-based rule mining in large, dense databases". Data Mining and Knowledge Discovery 4 (2): 217–240. doi:10.1023/A:1009895914772.
- ^ Webb, G. I. (2000). Efficient Search for Association Rules. In R. Ramakrishnan and S. Stolfo (Eds.), Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD-2000) Boston, MA. New York: The Association for Computing Machinery, pages 99-107. online access
- ^ a b http://www.dssresources.com/newsletters/66.php
- ^ T. Menzies, Y. Hu, "Data Mining For Very Busy People." IEEE Computer, October 2003, pgs. 18-25.
- ^ M. J. Zaki. (2001). SPADE: An Efficient Algorithm for Mining Frequent Sequences. Machine Learning Journal, 42, 31–60.
External links
Bibliographies
- Annotated Bibliography on Association Rules by M. Hahsler
- Statsoft Electronic Statistics Textbook: Association Rules
Implementations
- Pervasive DataRush, data mining platform for big data, includes association rule mining
- KXEN, a commercial Data Mining software
- Silverlight widget for live demonstration of association rule mining using Apriori algorithm
- RapidMiner, a free Java data mining software suite (Community Edition: GNU)
- Orange, a free data mining software suite, module orngAssoc
- Ruby implementation (AI4R)
- arules, a package for mining association rules and frequent itemsets with R.
- C. Borgelt's implementation of Apriori and Eclat
- Frequent Itemset Mining Implementations Repository (FIMI)
- Frequent pattern mining implementations from Bart Goethals
- Weka, a collection of machine learning algorithms for data mining tasks written in Java.
- KNIME an open source workflow oriented data preprocessing and analysis platform.
- Data Mining Software by Mohammed J. Zaki
- Magnum Opus, a system for statistically sound association discovery.
- LISp Miner, Mines for generalized (GUHA) association rules. Uses bitstrings not apriori algorithm.
- Ferda Dataminer, An extensible visual data mining platform, implements GUHA procedures ASSOC. Features multirelational data mining.
- STATISTICA, commercial statistics software with an Association Rules module.
- SPMF, Java implementations of 39 frequent itemset, sequential pattern, sequential rule, and association rule mining algorithms
- ARtool, GPL Java association rule mining application with GUI, offering implementations of multiple algorithms for discovery of frequent patterns and extraction of association rules (includes Apriori and FPgrowth)